ОПРЕДЕЛЕНИЕ СЕПАРАТРИСНЫХ ПОВЕРХНОСТЕЙ И ПРЕДЕЛЬНЫХ ЦИКЛОВ

Задачи нахождения уравнений сепаратрисных поверх­ностей и определения предельных циклов являются значительно более сложными, чем рассмотренные ранее задачи анализа движе-

CenapatpiicHbie поверхности и предельные циклы 139 ния в окрестности особых точек. Как отмечалось в гл. 3, в общем случае их не удается решить. Однако в рассматриваемом случае анализа уравнении нелинейного бокового движения сформулиро­ванные вопросы удается в определенной мере исследовать. В част­ности, возможно определение уравнения сепаратрисной поверх­ности в непосредственной близости особой точки, когда поверх­ность является плоскостью.

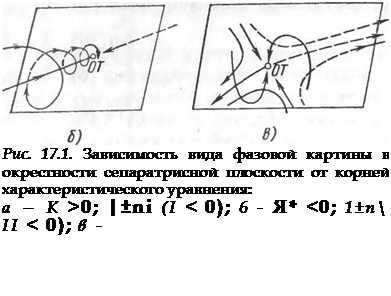
Когда характеристическое уравнение имеет третий порядок, возможны два вида значений корней: 1) один действительный, положительный или отрицательный корень и два комплексно- сопряженных корня; 2) три действительных корня. В рассматри­ваемой задаче обычно только один из трех действительных корней может быть положительным. Соответствующие этим случаям виды движения в окрестности сепаратрисной плоскости иллюстрируются рис. 17.1. На рис. 17.1, а показан вид движения в окрестное?!! особой точки (ОТ), когда действительный корень 0, а на

рис. 17.1, б, когда корень < 0. На рис. 17.1, в показан случай трех действительных корней, когда > О, Х2>3 < 0. Сепаратрис — ная плоскость на рис. 17.1, а разделяет фазовое пространство на две области, движение в которых имеет различные точки притя­жения. Сепаратрисная плоскость на рис. 17.1, б также разделяет фазовое пространство на области притяжения особых точек, и ее нахождение представляет практический интерес. Когда особая точка соответствует устойчивому движению, эта плоскость позво­ляет приближенно определить соотношение между параметрами движения самолета, так как часто | М > | £ | и движение, описы­ваемое действительным корнем, успевает быстро затухнуть и оста­ется колебательное движение, которое происходит в окрестности найденной плоскости. В том случае, когда движение в окрестности особой точки является колебательно-неустойчивым, то, как отме­чалось в гл. 3, в ее окрестности возникает предельный цикл, который приближенно располагается в найденной сепаратрисной плоскости.

Для нахождения уравнения сепаратрисной плоскости восполь­зуемся методикой, изложенной в гл. 3. Решение для фазовых

траекторий, лежащих на сепаратрнсной плоскости, не зависит от действительного корня X. В общем случае решение, например для параметра движения cov, может быть представлено в виде

(Од (т) — Лхе^ — J — А2ек-Т — f~ А3е^ту

где Хх — действительный корень; X2t Х3 — действительные либо комплексно-сопряженные корни; Лх, Л2, А3 -— постоянные, зави­сящие от начальных условий.

Решение в виде (17.1) соответствует всем фазовым траекториям в окрестности седловой особой точки. В качестве начальных усло­вий при этом могут быть взяты любые сочетания фазовых коорди­нат ©д., со^, р. Определим, при каких сочетаниях фазовых коорди­нат, рассматриваемых как начальные условия в решении (17.1), коэффициент Лх будет равен нулю. Как было показано в гл. 3, соответствующее уравнение будет уравнением сепаратрнсной плоскости.

Из решения (17.1) получим систему алгебраических уравнений для нахождения постоянных Лъ Л2, А3 в функции начальных условий:

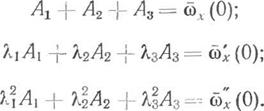(17.2)

Выражение для Лх в функции (о*(0), wi(0), со^(0) находится из соотношения

711 — Дх/ Доэ

где Д0 — характеристический определитель системы алгебраиче­ских уравнений (17.2), а Дх — определитель, получаемый из Д0 заменой первого столбца на столбец правых частей.

Поскольку нам необходимо найти Лх, а затем приравнять этот коэффициент нулю, то нет необходимости находить определитель Д0, достаточно знать определитель Дх:

(Од (0) 1 1

Дх = со* (0) Ху X,

" /Г\ л 2 л 2

(о* (0) А2 Аз

Раскрывая определитель (17.3) и приравнивая его нулю, получим

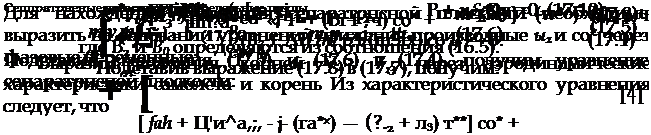Выражение (17.9) хотя и достаточно громоздкое, однако позволяет достаточно просто определять при известных значениях корня соответствующую сепаратриспую плоскость. Значение действи­тельного корня 7,г удобно находить, используя метод, изложенный в § 16. Для грубых оценок, уравнение для сепаратрнсной пло­скости для малого демпфирования можно приближенно пред­ставить в виде

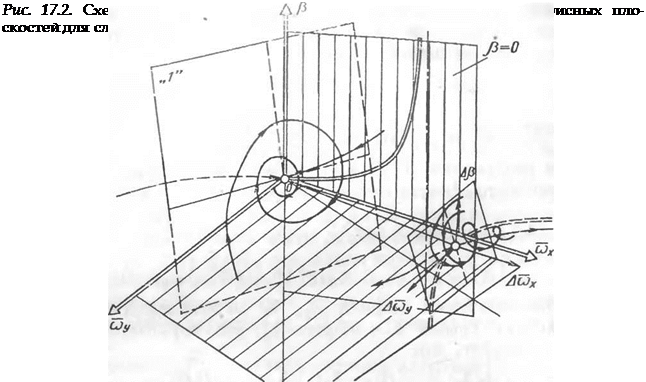
На рис. 17.2 приведена схема фазовой картины движения для самолета, сбалансированного на положительном угле атаки, и выделены найденные по описанной методике плоскость колебаний в окрестности устойчивости особой точки и сепаратрисная пло­скость, отделяющая область притяжения устойчивой особой точки от остального фазового пространства.

Уравнения бокового движения самолета (15.3) являются нелинейными уравнениями, и поэтому в них кроме устойчивого

либо неустойчивого движения в окрестности особых точек могут существовать режимы периодического движения — предельные циклы. Как отмечалось в гл. 3, при изменении типа особой точки от устойчивой к колебательно-неустойчивой всегда одновременно рождается периодическое движение — предельный цикл. Для нахождения таких режимов и определения условий их существо­вания воспользуемся методом гармонического баланса [9, 1, 7]. Анализ уравнений (15.3) в общем случае приводит к весьма гро­моздким выражениям, поэтому для получения результатов в до­статочно наглядном виде сохраним в уравнениях только наиболее существенные члены. В частности, пренебрежем влиянием на динамику самолета следующих коэффициентов сил и моментов,

приняв их равными нулю, с ~ту^ тх = 0.

Для использования метода гармонического баланса произведем преобразование уравнений (15.3) к новым переменным так, чтобы они имели особую точку, относительно которой рассматривается движение, в начале координат. С этой целью получим из (15.3) точные уравнения в вариациях относительно установившегося движения самолета, рассматривая параметры его движения в виде:

ю* = — + Aw. v;

Р — Рст “Ъ АР;

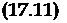
(Оу ©г/ст “Г А(‘)л.

Сепаратрисные поверхности и предельные циклы

Здесь рст, co^CT, Q — значения параметров движения самолета в особой точке.

Получим уравнения в вариациях:

АР’ — рДсо^ + ра0Дац;

Дсо*, = т™уА(йу + (ml + Bj. iQ2) Др

+ 2йрстВрДсоЛ. — f- 5ррст (Дсо*)2 + 2БрйДрДсоА. -{ БрДр (Дсо^2;

(17.12)

Аы’х — mf Др тхх Дсо*.

Приведем систему уравнений (17.12) к одному уравнению для вариации угловой скорости крена. Опустив для краткости записи знак вариации, получим

(х)х Botox V^l + Ctox Dtox) tox

— (fio CocOjc ~r Dqcdx) со* = 0, (17.13)

где B2, Bu B0 — коэффициенты линеаризованных уравнений движения (16.5);

С, = — 2Вц29.; С0 = — (вр2тРрст — 2Bytem**);

D — — Bp2; D0 = Bx2m/. (17.14)

Полученное при таких преобразованиях уравнение (17.13) является столь же точным как и (15.3) и позволяет исследовать движение не только в окрестности особой точки, но и во всем фазо­вом пространстве. Его особенностью является то, что оно записано относительно смещенной в фазовом пространстве точки, что позво­лило сделать это уравнение однородным (т. е. его особой точкой является начало координат). Пусть в окрестности этой особой точки существует предельный цикл и изменение параметров движения самолета близко к гармоническому, т. е.

со*a sinx. (17.15)

Решение (17.15) должно «в среднем» удовлетворять уравнению (17.13). Поэтому амплитуда и частота колебаний могут быть най­дены, если подставить решение (17.15) в уравнение (17.13), а затем, помножив его на sin vt и cos vt, проинтегрировать на интервале времени, равном периоду колебаний (Т = 2зт/v).

Выполнив интегрирование, получим систему алгебраических уравнений для нахождения величин а и v:

— В2v2 В0 — D0 — jj — сі2 = 0;

Из системы алгебраических уравнений (17.16) получим фор­мулу для нахождения амплитуды а на предельном цикле:

Учитывая выражения для D(), Dx (17.14) и тот факт, что В2Вг — — В0 = R (см. (16.7)), получим в окончательном виде формулу для нахождения амплитуды

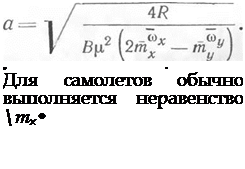(17.18)

Поэтому из (17.18) следует, что необходимым условием существо­вания предельного цикла является колебательная неустойчивость движения при малых возмущениях (R <С 0). Из полученных результатов следует, что если в окрестности особой точки решение колебательно-неустойчиво, то оно при увеличении амплитуды переходит в предельный цикл. Частота колебаний на предельном цикле при известной величине амплитуды колебаний может быть найдена из второго уравнения системы (17.16):

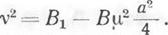(17.19)

Из формулы (17.19) видно, что частота колебаний при малых амплитудах (а ~ 0) близка к частоте собственных боковых колеба­ний

(17.20)

и убывает при возрастании амплитуды колебаний. Характер дви­жения в окрестности особой точки нетрудно представить. Как было получено в § 16,

которые подходят сверху и снизу, наматываются на один и тот же предельный цикл соответственно над или под сепаратрисной плоскостью. Способ нахождения соответствующей плоскости был изложен ранее.

На рис. 17.4 приведены примеры фазовых траекторий на пло­скости со*, р для случая а0 >> 0 (сор/соа -* 0), полученные расчет­ным путем. Из рисунка видно, что по мере увеличения отклонения элеронов (момента ДтЛ) возрастает колебательность движения, и при некотором значении Ат*х движение становится неустойчивым «в малом» и реализуется предельный цикл. При дальнейшем увели­чении управляющего момента Дгпх степень неустойчивости воз­растает и амплитуда предельного цикла увеличивается, что подтверждает результаты, полученные ранее.

Полученный ранее результат, заключающийся в том, что боко­вое движение при наличии колебательной неустойчивости стре­мится к предельному циклу, имеет вполне определенные подтверж­дения в летных испытаниях. Некоторые примеры таких движений приведены в гл. 7—9.

Как следует из проделанного анализа, причиной возникнове­ния предельного цикла являются нелинейные инерционные и кине­матические члены в уравнениях движения при линейных аэродина­мических характеристиках. Нелинейности в аэродинамических характеристиках могут оказать определенное влияние на пара­метры предельного цикла, но основные его закономерности сохра­нятся. В этой связи следует отметить, что движение типа предель­ного цикла часто наблюдается и в записях результатов летных испытаний самолетов на штопор.